Learn to Solve Rubik's Cube Puzzles Using 3 Simple Tricks
|
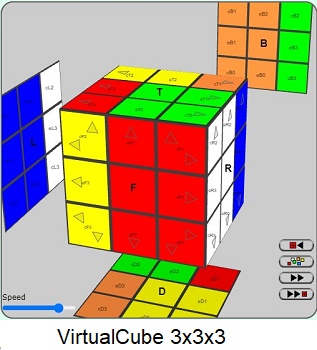
Rubik's Cube 3x3x3
Learn to Solve Rubik's cube using 3 Simple Tricks: Trick1, Trick2, Trick3.
with interactive step-by-step animation accompanied by dynamic detailed description of every move.
We tell you beforehand what is next to be done and you can click to see the animation, step by step.
You can undo, replay, save and much more.
|
|
||||||||
|
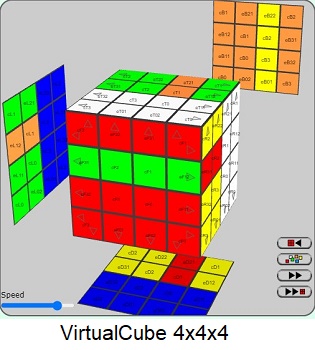
Rubik's Cube 4x4x4
Learn to Solve Rubik's cube using 4 Simple Tricks: Trick1, Trick2, Trick3, Trick4.
with interactive step-by-step animation accompanied by dynamic detailed description of every move.
We tell you beforehand what is next to be done and you can click to see the animation, step by step.
You can undo, replay, save and much more.
|
|
||||||||
| |||||||||
|
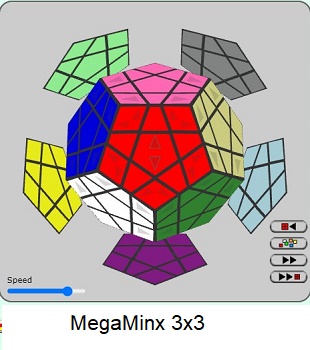
MegaMinx 3x3
Learn to Solve MegaMinx 3x3 using 3 Simple Tricks: Trick1, Trick2, Trick3.
with interactive step-by-step animation accompanied by dynamic detailed description of every move.
We tell you beforehand what is next to be done and you can click to see the animation, step by step, repeat and replay.
|
|
||||||||
|
MegaMinx 4x4
Learn to Solve MegaMinx 4x4 using same Tricks for solving MegaMinx 3x3.
with interactive step-by-step animation accompanied by dynamic detailed description of every move.
We tell you beforehand what is next to be done and you can click to see the animation, step by step, repeat and replay.
|

|
||||||||
| |||||||||